Raisonnements

Un raisonnement mathématique est un processus permettant d'établir, à partir de propositions vraies, de nouvelles propositions, de nouveaux résultats en utilisant des principes logiques. Dans cette partie, nous étudions différents types de raisonnement.

Contenu.

Raisonnement par implication
Raisonnement par équivalence
Raisonnement par équivalence en deux temps.
Raisonnement par contraposition
Raisonnement par l'absurde
Raisonnement par disjonction des cas
Méthode par exhaustion
Raisonnement par analyse-synthèse
Raisonnement par récurrence

Bibliographie

Langage mathématique

Expressions mathématiques et Exemples d'expressions mathématiques
Variables libres, variables liées
Assertions ou Propositions
Connecteurs : NON, ET et OU
Implication, équivalence
Négation d'une assertion utilisant un connecteur et Tables de vérité
Condition nécessaire, condition suffisante.
Quantificateurs, première partie
Quantificateurs, deuxième partie
Négation d'une assertion utilisant des quantificateurs
Contraposée et réciproque

Expressions mathématiques

Le langage mathématique est formé d'expressions mathématiques, qui sont des assemblages de signes qui obéissent à certaines règles.

L'assemblage «

y ⩾

» n'est pas une expression mathématique, car le signe

⩾

est un signe qui ne s'utilise qu'entre deux éléments (par exemple deux réels). Par contre, «

y ⩾ 2

», ou «

y ⩾ x

», ou « si

y ⩾ 2

, alors

y^{2} ⩾ 4

» sont des expressions mathématiques.

Définition. On classe les expressions mathématiques en deux grandes catégories.

les expressions qui servent à désigner des objets mathématiques; nous les appellerons des termes ;
les expressions qui sont des affirmations de faits concernant des objets mathématiques; nous les appellerons des propositions ou assertions

Définition. On dit que deux expressions mathématiques sont synonymes si

ou bien ce sont deux termes et ces deux termes désignent le même objet quelles que soient les circonstances;
ou bien ce sont deux propositions et ces deux propositions sont en même temps vraies et en même temps fausses, quelles que soient les circonstances.

Dans le cas des propositions, on dit souvent équivalentes au lieu de synonymes.

Des exemples sont à la page suivante.

Exemples d'expressions mathématiques

Considérons les expressions suivantes. Ce sont toutes des expressions mathématiques au sens donné ici , et dans chacune d'elles la variable $x$ désigne un nombre réel.

${x \in ℝ ∣ x^{2} = 1}$
$x^{2} = 1$
$x^{3} = 1$ ou $x^{3} = - 1$
${- 1; 1}$
$x = 1$ ou $x = - 1$
pour tout réel $x$ , si $x^{2} = 1$ alors $x = 1$ ou $x = - 1$

Les expressions 1 et 4 sont des termes (qui désignent ici des ensembles), les expressions 2, 3 , 5 et 6 sont des propositions.

Les deux termes 1 et 4 sont synonymes car ils désignent exactement le même objet.
Les propositions 2, 3 et 5 sont équivalentes, elles sont vraies exactement pour les mêmes valeurs (1 et -1) substituées à la variable $x$ , et fausses pour les autres.
La proposition 6 est une proposition vraie, nous y reviendrons plus loin.

Ces exemples nous montrent que dans la constitution d'expressions mathématiques, termes et propositions peuvent être imbriqués : pour constituer le terme ${x \in ℝ ∣ x^{2} = 1}$ , on a utilisé la proposition $x^{2} = 1$ .

Assertions ou Propositions

Définition. Une assertion, appelée encore proposition, est un énoncé dont on peut dire, avec certitude, s'il est vrai ou faux (sa valeur de vérité). En particulier tous les termes qui la composent doivent être soigneusement définis pour qu'il n'y ait pas d'ambiguité et que l'assertion soit "complète".

Exemples.

Il est jaune n'est pas une assertion : je ne pourrai jamais décider si "il" est jaune ou pas, tant que je ne sais pas de quoi il s'agit.
Le stylo de Marianne est noir est une assertion (du moins s'il n'y a qu'une seule Marianne et qu'elle n'a qu'un seul stylo).
$x$ est plus grand que $y$ n'est pas une assertion. Elle est incomplète puisque x et y ne sont pas connus
Monsieur Martin est un homme brun ou Tous les hommes sont bruns sont des assertions.
$n^{2} \geq 4$ n'est pas une assertion complète. De quels $n$ s'agit-il ?
Tous les entiers naturels vérifient $n^{2} \geq 4$ est une assertion (fausse mais une assertion quand même !)
$x^{4} - 2 x^{2} + 1 = 0$ n'est pas une assertion. Sa valeur de vérité n'est pas fixe..
$x > 1$ n'est pas une assertion, mais soit $x \in ℝ, x > 1$ en est une...
Tout entier pair supérieur à 3 est la somme de deux nombres premiers. Là, on n'en sait rien encore... Conjecture de Goldbach !!

Cependant, tous les exemples qui précèdent et qui sont pris dans le langage courant peuvent être sujets à caution, comme on le verra dans certains exemples qui suivent. Ils servent ici à faire le passage avec les mathématiques.
Par ailleurs, en mathématiques, on fait souvent ce qu'on appelle des abus de langage.

Une différence entre le langage courant et les mathématiques est la suivante : tout ce qui n'est pas "vrai" (au sens de la logique) ne doit pas être utilisé dans un raisonnement. Il n'y a donc pas de sous-entendu comme on le fait fréquemment dans la vie courante. Par exemple, l'affirmationLes filles de ce cours sont excellentes ne dit, ni ne prétend rien sur le niveau des garçons, comparativement. Le français peut faire, là, d'autres suppositions !!..

Exercice. Assertion complète ou incomplète

Connecteurs : NON, ET et OU

Les connecteurs permettent de composer de nouvelles assertions. La valeur de vérité de l'assertion obtenue s'exprime, à l'aide d'une table de vérité, en fonction des valeurs de vérité de celles qui la constituent. On définit dans cette page les connecteurs NON, ET et OU.

Définitions. Soient

𝒫

𝒬

des assertions. Les assertions NON

𝒫

(ou négation de

𝒫

𝒫

𝒬

(conjonction de

𝒫

𝒬

, noté aussi

𝒫 \land 𝒬

) et

𝒫

𝒬

(disjonction de

𝒫

𝒬

, noté aussi

𝒫 \lor 𝒬

) ont pour tables de vérité :

$𝒫$	$𝒬$	NON $𝒫$	$𝒫$ ET $𝒬$	$𝒫$ OU $𝒬$
V	V	F	V	V
V	F	F	F	V
F	V	V	F	V
F	F	V	F	F

Remarques.

(NON $𝒫$ ) est vraie si $𝒫$ est fausse, et fausse si $𝒫$ est vraie.
A l'aide d'une table de vérité, on montre : NON (NON $𝒫$ ) est équivalente à $𝒫$ . Les deux propositions ont la même valeur de vérité.
La logique classique respecte la règle du tiers exclu : Une assertion $𝒫$ est soit vraie, soit fausse.
L'assertion $𝒫$ ET $𝒬$ est vraie si et seulement si les deux assertions $𝒫$ et $𝒬$ sont vraies.
L'assertion $𝒫$ OU $𝒬$ est fausse si et seulement si les deux assertions $𝒫$ et $𝒬$ sont fausses.

Exemples.

La négation de « $x \geq 2$ » est : « $x < 2$ ».
La proposition «10 est divisible par 3, ou 10 est pair » est vraie car l'une des deux propositions qui la compose est vraie.
La proposition « $x$ est divisible par $3$ , et $x$ est pair» n'est vraie que si les deux propositions sont simultanément vraies, c'est-à-dire lorsque $x$ est un multiple de $6$ .
La proposition « $x$ est divisible par $3$ , ou $x$ est pair» n'est fausse que lorsque l'une et l'autre des deux propositions sont fausses, c'est-à-dire lorsque $x$ est un nombre impair non multiple de $3$ .

Exercices.

Déterminer la table de vérité d'une proposition.

Deux propositions avec NON, ET, OU
Trois propositions avec ET, OU

Reconnaître la table de vérité d'une proposition.

Deux propositions avec NON, ET, OU
Trois propositions avec ET, OU

Implication, équivalence

Définition. Soient

𝒫

𝒬

des assertions. L'assertion

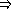
𝒫 \Rightarrow 𝒬

(qui se lit

𝒫

implique

𝒬

) a la table de vérité suivante.

$𝒫$	$𝒬$	$𝒫$ $Rightarrow$ $𝒬$
V	V	V
V	F	F
F	V	V
F	F	V

Remarque. Soit

𝒫

une proposition fausse, alors, quelle que soit la valeur de vérité de la proposition

𝒬

(vraie ou fausse), l'implication

𝒫

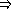$Rightarrow$

𝒬

est vraie...

Propriété. L'assertion

𝒫 \Rightarrow 𝒬

est équivalente à l'assertion (NON

𝒫

) OU

𝒬

Preuve. Il suffit de comparer les tables de vérité des deux assertions.

Définition. L'assertion

𝒫 \Leftrightarrow 𝒬

(qui se lit

𝒫

est équivalente à

𝒬

) est l'assertion [

(𝒫 \Rightarrow 𝒬

) ET (

𝒬 \Rightarrow 𝒫

)]

L'assertion " $𝒫$ est équivalent à $𝒬$ " est vraie si et seulement si les deux assertions sont soit simultanément vraies, soit simultanément fausses.

Exercices.

Déterminer la table de vérité d'une proposition.

Implication et négation de propositions
Trois propositions avec implication, ET, OU

Reconnaître la table de vérité d'une proposition.

Implication et négation de propositions
Trois propositions avec implication, ET, OU

Négation d'une assertion utilisant un connecteur

Propriétés. Soient

𝒫

𝒬

des assertions.

La négation de l'assertion $[𝒫$ ET $𝒬$ ] est l'assertion : [(NON $𝒫$ ) OU (NON $𝒬$ )]
La négation de l'assertion $[𝒫$ OU $𝒬$ ] est l'assertion : [(NON $𝒫$ ) ET (NON $𝒬$ )]
La négation de l'assertion $[𝒫 \Rightarrow 𝒬$ ] est l'assertion : $[𝒫$ ET (NON $𝒬$ )] .

Ces propriétés se démontrent à l'aide de tables de vérité.

Exemple 1. Dans la table ci-dessous, on lit, dans les trois colonnes de gauche, les valeurs de $𝒫$ , $𝒬$ et [ $𝒫$ ET $𝒬$ ] et, dans les trois de droite, celles de [NON $𝒫$ ], [NON $𝒬$ ] et [NON $𝒫$ OU NON $𝒬$ ]. En considérant les deux colonnes du milieu, on constate que [NON $𝒫$ OU NON $𝒬$ ] est bien la négation de [ $𝒫$ ET $𝒬$ ].

$𝒫$	$𝒬$	$𝒫$ et $𝒬$	NON $𝒫$ OU NON $𝒬$	NON $𝒫$	NON $𝒬$
V	V	V	F	F	F
V	F	F	V	F	V
F	V	F	V	V	F
F	F	F	V	V	V

On en déduit facilement que la négation de [ $𝒫$ OU $𝒬$ ] est [NON $𝒫$ ET NON $𝒬$ ].

Exemple 2. Dans la table ci-dessous, on démontre que [ $𝒫$ ET NON $𝒬$ ] est la négation de [ $𝒫 \Rightarrow 𝒬$ ] qui est définie comme [NON $𝒫$ OU $𝒬$ ].

$𝒫$	$𝒬$	NON $𝒫$	NON $𝒬$	$𝒫 \Rightarrow 𝒬$	$𝒫$ ET NON $𝒬$
V	V	F	F	V	F
V	F	F	V	F	V
F	V	V	F	V	F
F	F	V	V	V	F

On notera que la négation d'une implication n'est pas une implication !

Exemples.

La négation de l'assertion $(x \geq 1)$ ET $(x < 4)$ est l'assertion $(x < 1)$ OU $(x \geq 4)$ .
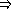La négation de l'assertion ( $n$ est pair) $Rightarrow$ ( $n$ est divisible par $4$ ) est l'assertion ( $n$ est pair) ET ( $n$ n'est pas divisible par $4$ ).

Exercices. Soient

𝒫

𝒬

ℛ

des assertions. Donner la négation des assertions suivantes :

$𝒫$ OU $𝒬$ OU $ℛ$

(NON $𝒫$ ) ET (NON $𝒬$ ) ET (NON $ℛ$ )
$(x^{2} = 1) \Rightarrow [(x = 1) OU (x = - 1)]$

$(x^{2} = 1)$ ET $(x \neq 1)$ ET $(x \neq - 1)$

Condition nécessaire, condition suffisante.

Définitions. Soient

𝒫

𝒬

des assertions.

Si $𝒫 \Rightarrow 𝒬$ , on dit que
- $𝒫$ est une condition suffisante de $𝒬$
- $𝒬$ est une condition nécessaire de $𝒫$
Si $𝒫 \Leftrightarrow 𝒬$ , on dit que $𝒫$ est une condition nécessaire et suffisante de $𝒬$ (et réciproquement).

Remarque: Les cinq énoncés suivants ont la même signification.

$𝒫 \Rightarrow 𝒬$
Pour que $𝒫$ soit vraie, il faut que $𝒬$ soit vraie.
Pour que $𝒬$ soit vraie, il suffit que $𝒫$ soit vraie.
$𝒬$ est une condition nécessaire pour avoir $𝒫$ .
$𝒫$ est une condition suffisante pour avoir $𝒬$ .

Exercice. Condition nécessaire ou condition suffisante .

Négation d'une assertion utilisant des quantificateurs

Propriétés. Soit

A

un ensemble et

P (x)

une expression dépendant d'un variable

x

La négation de l'assertion $[\forall x \in A, P (x)$ ] est l'assertion $[\exists x \in A, NON P (x)$ ].
La négation de l'assertion $[\exists x \in A, P (x)$ ] est l'assertion $[\forall x \in A, NON P (x)$ ].

Règle pratique : Si, dans une proposition figurent des quantificateurs et une proposition

𝒫

, alors dans la négation de cette proposition, le quantificateur

\forall

, (resp.

\exists

) se transforme en

\exists

(resp.

\forall

) , et la proposition

𝒫

devient (NON

𝒫

)

Exemple 1. La négation de $« \forall x \in ℕ, x$ est multiple de 4 » est $« \exists x \in ℕ, x$ n'est pas multiple de 4 » .

Exemple 2. La négation de $« \exists x \in X, x < 3 »$ est $« \forall x \in X, x \geq 3$ » .

Exemple 3. Écrire à l'aide de quantificateurs les phrases suivantes (avec des variables prenant leurs valeurs dans l'ensemble $G$ des guichets et dans l'ensemble $J$ des jours)

$𝒫$ : tous les guichets sont fermés certains jours.
$𝒬$ : certains jours tous les guichets sont fermés.

Puis écrire leur négation en langage courant et avec des quantificateurs.

Solution

( $𝒫$ ) : Tous les guichets sont fermés certains jours.

$\forall g \in G, \exists j \in J$ , $g$ est fermé le jour $j$

( $𝒬$ ) : Certains jours tous les guichets sont fermés.

$\exists j \in J, \forall g \in G,$ $g$ est fermé le jour $j$

(non $𝒫$ ) : Certains guichets sont ouverts tous les jours.

$\exists g \in G, \forall j \in J,$ $g$ est ouvert le jour $j$

(non $𝒬$ ) : Tous les jours, un guichet (au moins) est ouvert.

$\forall j \in J, \exists g \in G,$ $g$ est ouvert le jour $j$

Vous pouvez remarquer que c'est plutôt plus simple mathématiquement :

on remplace $\exists$ par $\forall$ ,
on remplace $\forall$ par $\exists$
et on remplace l'assertion g est fermé par sa négation qui est ici l'assertion g est ouvert

Exercices.

Le langage courant utilise souvent des quantificateurs. Essayer de les détecter et donner la négation des assertions qui les utilisent dans l'exercice suivant : Négation de propositions dans le langage courant
Un quantificateur 1
Un quantificateur 2
Un quantificateur et un connecteur
Un quantificateur et une implication
Négation de proposition avec deux quantificateurs

Contraposée et réciproque

Définition. Soient

𝒫

𝒬

des assertions.

La contraposée de l'implication $𝒫 \Rightarrow 𝒬$ est l'implication $NON 𝒬 \Rightarrow NON 𝒫$ .
La réciproque de l'implication $𝒫 \Rightarrow 𝒬$ est l'implication $𝒬 \Rightarrow 𝒫$ .

Propriété : Une implication et sa contraposée ont les mêmes valeurs de vérité. Les assertions

[𝒫 \Rightarrow 𝒬

] et [NON

𝒬 \Rightarrow

NON

𝒫

] sont logiquement équivalentes.

Démonstration. D'une part, $𝒫 \Rightarrow 𝒬$ est par définition la proposition [NON $𝒫$ OU $𝒬$ ]. Et d'autre part, [NON $𝒬 \Rightarrow$ NON $𝒫$ ] est la proposition : [NON(NON $𝒬$ ) OU NON $𝒫$ ], c'est à dire : $[𝒬$ OU NON $𝒫$ ]. C'est bien la même chose.

Dans certains cas, la propriété contraposée peut être sensiblement plus facile à démontrer que la propriété elle-même ; c'est le raisonnement par contraposée .

Exercice.
Démontrer l'équivalence entre

𝒫 \Rightarrow 𝒬

[NON 𝒬 \Rightarrow NON 𝒫

] en utilisant des tables de vérité .

Attention à ne pas confondre la contraposée d'une implication avec sa réciproque.

Exemples.

Considérons la propriété : « si $n \in ℕ$ est divisible par 4, alors il est pair » (Proposition vraie)
- Sa contraposée est : si $n \in ℕ$ est impair, alors, il n'est pas divisible par 4. (Proposition aussi vraie que la première)
- Sa réciproque est : si $n \in ℕ$ est pair, alors, il est divisible par 4. (Proposition fausse...)
Donnons un exemple en langage courant : S'il pleut, le sol est mouillé.
- Sa contraposée est : si le sol n'est pas mouillé, il ne pleut pas énoncée plus couramment : Si le sol est sec, il ne pleut pas. Ces deux implications sont vraies et équivalentes.
- La réciproque de la première est si le sol est mouillé, il pleut.
  Et cette implication est fausse, car le sol peut être mouillé par le passage du camion municipal de nettoyage ou bien par de la neige qui a fondu.

Exercices.

contraposées et réciproques dans le langage courant.
contraposées et réciproques en mathématiques.

Attention quand même aux pièges de la vie courante !

Contraposée et réciproque : pièges de la vie courante

En fait dans la vie courante on confond très souvent (à tort) contraposée et réciproque, en induisant des sous-entendus qui n’existent pas. Par exemple, si l'on vous dit :

Si tu es sage ce matin, tu auras du chocolat cet après-midi

[Notons tout de suite, et c'est important, que cela ne dit rien de ce qui se passera si l'on n'a pas été sage le matin....]

la contraposée est

Si tu n'as pas de chocolat cet après-midi, tu n'as pas été sage ce matin

et la réciproque

Si tu as du chocolat cet après-midi, tu as été sage ce matin.

Enfin, la contraposée de la réciproque est

Si tu n'es pas sage ce matin, tu n'auras pas de chocolat cet après-midi.

Ce qui n'est pas équivalent à la première phrase. Mais c'est en général cette dernière affirmation qui est dans la tête de celui qui prononce la première (en appliquant des principes d'éducation positive !)

Raisonnements

Raisonnement par implication
Raisonnement par équivalence
Raisonnement par équivalence en deux temps.
Raisonnement par contraposition
Raisonnement par l'absurde
Raisonnement par disjonction des cas
Méthode par exhaustion
Raisonnement par analyse-synthèse
Raisonnement par récurrence

Raisonnement par implication

Deux règles fondamentales fondent les raisonnements :

Principe de déduction. Si

𝒫

est vraie et si

𝒫 \Rightarrow 𝒬

est vraie, alors l'assertion

𝒬

est vraie.

Cette règle utilise la définition de la vérité d'une implication. On l'emploie souvent sans revenir à cette définition.
Remarque : Si $𝒫$ est fausse, alors quelle que soit la valeur de vérité de $𝒬$ , l'implication $𝒫 \Rightarrow 𝒬$ est toujours vraie et ne fournit donc aucun renseignement sur $𝒬$ .
Dans la pratique, le raisonnement commence donc par : "Supposons que $𝒫$ est vraie", et on démontre ensuite que $𝒬$ l'est aussi.

Exercice 1. Démontrer l'implication :

x^{2} = x \Rightarrow ∣ x ∣ = x

Exemple 2. Soit

A B C

un triangle dont les cotés de

ABC

ont pour mesure :

A B = 4

A C = 3

B C = 5

. C'est l'assertion

𝒫

.
L'assertion

𝒬

est : le triangle est rectangle.
La réciproque du théorème de Pythagore nous indique que si dans un triangle:

A B^{2} + A C^{2} = B C^{2}

, alors ce triangle est un triangle rectangle. (

𝒫 \Rightarrow 𝒬

)
Conclusion : l'assertion

𝒬

est vraie :

A B C

est un triangle rectangle

Exemple 3.

Considérons une fonction $f$ définie sur $ℝ$ .
On note $𝒫$ l'assertion : $f$ est dérivable sur $ℝ$ .
On note $𝒬$ l'assertion : $f$ est continue sur $ℝ$ .
L'assertion $𝒫 \Rightarrow 𝒬$ est le théorème : Toute fonction dérivable sur $ℝ$ est continue sur $ℝ$ .

Supposons que $𝒫$ soit vraie pour une fonction $f$ donnée.
$𝒫 \Rightarrow 𝒬$ est vraie (c'est le théorème)

Conclusion : la fonction

f

est continue sur

ℝ

Remarque : Dans la pratique, on est souvent conduit à utiliser plusieurs fois de suite la règle, on a ainsi :
Si $𝒫$ est vraie, si $𝒫 \Rightarrow 𝒬$ vraie, si $𝒬 \Rightarrow ℛ$ est vraie, alors $ℛ$ est vraie

Raisonnement par équivalence

Première méthode pour prouver une équivalence :

En s'appuyant sur la définition de l'équivalence de deux propositions , on énonce la règle suivante.

Règle 2. Pour démontrer qu'une proposition

𝒜

est vraie, on peut établir que

𝒜

est équivalente à une autre proposition

ℬ

, connue comme vraie.

Plus généralement, pour démontrer que $𝒫 \Leftrightarrow 𝒬$ , on peut aussi établir ainsi une suite d'équivalence entre la première propriété $𝒫$ et la propriété $𝒬$ , On aura ainsi :

$𝒫 \Leftrightarrow 𝒫_{1} \Leftrightarrow 𝒫_{2} \Leftrightarrow . . . . . \Leftrightarrow 𝒫_{n} \Leftrightarrow 𝒬$

On utilise souvent cette règle pour :

La résolution d'une équation, d'une inéquation.
De façon générale pour la détermination de l'ensemble des éléments vérifiant une propriété.

Remarque : Il convient d'être très prudent dans l'établissement des équivalences successives.

Exemple d'erreur :

On veut résoudre dans $ℝ$ , l'équation : $x + 1 = \sqrt{- 2 x + 6}$ . Pour que cette équation ait un sens, $x$ doit vérifier : $- 2 x + 6 \geq 0$ et $x + 1 \geq 0$ . On verra plus loin, que si cette équation a des solutions, l'une des inégalités est automatiquement vérifiée.

"Solution fausse" : "On élève au carré les deux membres", on obtient l'équation du second degré $x^{2} + 4 x - 5 = 0$ , que l'on résout, ce qui conduit à deux solutions -5 et 1. Si l'on vérifie dans l'équation, on voit que -5 ne convient pas... Que s'est-il passé ? Réponse : on n'a pas raisonné par équivalence !!

La bonne solution impose de formuler le problème avec l'équivalence suivante, en n'oubliant pas les deux conditions :

$x + 1 = \sqrt{- 2 x + 6} \Leftrightarrow {\begin{matrix} (x + 1)^{2} = - 2 x + 6 \\ x + 1 \geq 0 \\ - 2 x + 6 \geq 0 \end{matrix}$

La deuxième condition

- 2 x + 6 \geq 0

est inutile, car comme

- 2 x + 6

est égal à un carré (première ligne), elle est satisfaite.

$x + 1 = \sqrt{- 2 x + 6} \Leftrightarrow {\begin{matrix} (x + 1)^{2} = - 2 x + 6 \\ x + 1 \geq 0 \end{matrix} \Leftrightarrow {\begin{matrix} x^{2} + 4 x - 5 = 0 \\ x + 1 \geq 0 \end{matrix}$

Et on résout le système, sans oublier l'inéquation, ce qui conduit alors au résultat correct : L'équation n'a qu'une seule solution qui vaut 1.

Raisonnement par équivalence en deux temps.

Deuxième méthode pour prouver une équivalence :

Règle : On démontre la proposition

𝒫 \Leftrightarrow 𝒬

en prouvant successivement les deux implications

𝒫 \Rightarrow 𝒬

𝒬 \Rightarrow 𝒫

Exemple 1. Soit

z

un nombre complexe. Montrons qu'il est réel si et seulement s'il est égal à son conjugué.

Sens direct : Si $z$ est un nombre complexe, il existe $a$ et $b$ réels tels que $z = a + ib$ . Son conjugué est $\bar{z} = a - ib$ . Si $z$ est réel, sa partie imaginaire est nulle et donc $b = 0$ . Ainsi $z = a$ et $\bar{z} = a$ . L'égalité $z = \bar{z}$ est démontrée.

Réciproquement : Si $z = \bar{z}$ , $a + ib = a - ib$ . On a ainsi $2 b = 0$ , puis $b = 0$ , et donc $z = a$ qui est donc un nombre réel.

L'équivalence est maintenant démontrée.

Exemple 2. Montrer que :

(a + b)^{2} = a^{2} + b^{2}

si et seulement

a = 0

b = 0

Sens direct : En développant l'expression, on trouve $2 a b = 0$ , et donc $a = 0$ ou $b = 0$ .

Réciproquement : En remplaçant $a$ et $b$ par 0 dans l'expression, on vérifie que les deux membres valent tous les deux zéro, d'où l'égalité.

L'équivalence est maintenant démontrée.

Raisonnement par contraposition

On a vu, dans le paragraphe précédent Contraposée et réciproque , qu'une implication et sa contraposée sont équivalentes.

Règle 3. Pour démontrer une implication, il suffit de démontrer sa contraposée.

En d'autres termes, pour démontrer une implication, on peut le faire soit directement, soit en démontrant sa contraposée. En effet, la propriété contraposée peut être sensiblement plus facile à démontrer que la propriété elle-même, comme le montre le cas suivant.

Exemples.

Pour démontrer que l'implication portant sur des nombres réels :
$a b \neq 0 \Rightarrow [a \neq 0$ et $b \neq 0]$
est vraie, il est équivalent, et beaucoup plus simple, de vérifier que la contraposée :
$[a = 0$ ou $b = 0] \Rightarrow [a b = 0]$
est vraie, ce qui est évident.
Démontrer la proposition : $\forall n \in ℕ$ , $n^{2}$ impair $\Rightarrow n$ impair.

Pour démontrer cette implication, il est plus simple de démontrer la contraposée : $\forall n \in ℕ$ , $n$ pair $\Rightarrow n^{2}$ pair.
Ce qui ne présente aucune difficulté. Si $n$ est pair, il existe $n \in ℕ$ tel que $n = 2 p$ . On obtient $n^{2} = (2 p)^{2} = 4 p^{2}$ donc le nombre $n^{2}$ est pair.

Exercice 1.
Démontrer la proposition : Soit

x \in ℝ [\forall ε \in ℝ_{+}^{*}, ∣ x ∣ < ε] \Rightarrow [x = 0]

Exercice 2.
Démontrer la proposition :

\forall n \in ℕ

, [ si

n^{2} - 1

n'est pas divisible par 8, alors

n

est pair].

Raisonnement par l'absurde

Le raisonnement par l'absurde consiste à supposer comme hypothèse la négation de ce que l'on veut démontrer, puis, par des déductions logiques utilisant cette hypothèse, à aboutir à une contradiction ou une absurdité.

Le raisonnement par l'absurde pour démontrer la proposition

𝒫

peut donc se formaliser ainsi :
Si

[(NON 𝒫) \Rightarrow 𝒬]

est vraie et si

𝒬

est une proposition fausse, alors on peut affirmer que

𝒫

est vraie.
En effet : Si

[(NON 𝒫) \Rightarrow 𝒬]

(qui est équivalent à

[𝒫 OU 𝒬]

) est vraie, avec

𝒬

fausse, c'est que

𝒫

est vraie.

Exemple : On veut démontrer que

\sqrt{2}

n'est pas un rationnel. Pour cela, on va supposer que

\sqrt{2}

est rationnel. Il existe donc deux entiers naturels

p

q

, premiers entre eux tels que :

\sqrt{2} = \frac{p}{q}

.
De l'équation

p^{2} = 2 q^{2}

, on déduit que

p

q

sont pairs:
En effet

p^{2}

est pair donc

p

également (ceci découle du fait que la contraposée :

p

impair

\Rightarrow p^{2}

impair est vraie, (voir page précédente où cela a été démontré pour les nombres pairs)).
Si

p

est pair, il existe

k \in ℕ

tel que

p = 2 k

. L'équation

p^{2} = 2 q^{2}

devient

4 k^{2} = 2 q^{2}

, soit

2 k^{2} = q^{2}

. Donc

q^{2}

est pair et en reprenant le même chose que ci dessus,

q

est pair.

p

q

sont donc tous les deux pairs.
Ce qui est en contradiction avec le choix de

p

q

qu'on a fait (premiers entre eux). D'où la contradiction, ce qui démontre que

\sqrt{2}

est un irrationnel.

Exercice.
Montrer qu'il existe une infinité de nombres premiers.

Aide. Supposons qu'il existe un nombre FINI de nombres premiers

p_{1}, p_{2}, . . . ., p_{n}

. On suggère de s'intéresser au nombre

N = p_{1} p_{2} . . . . p_{n} + 1

et au théorème de décomposition de tout entier naturel

n \geq 2

en produit de nombres premiers, pour faire apparaître une contradiction.

Un raisonnement par l'absurde pour montrer une implication peut parfois être remplacé par un raisonnement par contraposition. Par exemple,

on veut démontrer que $𝒫 \Rightarrow 𝒬$ est vraie,
on suppose (NON $𝒬$ ) ET $𝒫$ ,
on finit par démontrer non $𝒫$ et on se dit en contradiction avec $𝒫$ .

Mais si $𝒫$ ne nous a pas servi, on a en fait démontré : $NON (𝒬) \Rightarrow NON (𝒫)$ et donc $𝒫 \Rightarrow 𝒬$ par contraposition.

Raisonnement par disjonction des cas

Règle. Pour montrer une propriété par disjonction des cas, on la prouve dans le nombre fini des cas couvrant toutes les situations possibles. On traite ces cas les uns après les autres.

Exemple 1. Montrer que par disjonction des cas que :

\forall n \in ℕ \frac{n (n + 1)}{2}

est un entier naturel.

Deux cas seulement sont possibles: soit

n

est pair, soit il est impair.

Si $n$ est pair, il existe $p$ dans $ℕ$ tel que $n = 2 p$ et $\frac{n (n + 1)}{2} = \frac{2 p (2 p + 1)}{2} = p (2 p + 1)$ qui est un entier naturel.
Si $n$ est impair, il existe $p'$ dans $ℕ$ tel que $n = 2 p' + 1$ et $\frac{n (n + 1)}{2} = \frac{(2 p' + 1) (2 p' + 2)}{2} = (2 p' + 1) (p' + 1)$ qui est un entier naturel.

Exemple 2. Montrer qu'il existe deux irrationnels

a

b

tels que

a^{b}

soit rationnel.

Raisonner selon que

{\sqrt{2}}^{\sqrt{2}}

est rationnel ou non.

Solution

Rappelons que

\sqrt{2}

est irrationnel. Soit

{\sqrt{2}}^{\sqrt{2}}

est rationnel, soit il ne l'est pas et alors il est irrationnel.

Si ${\sqrt{2}}^{\sqrt{2}}$ est rationnel, on a fini. Les nombres a= $\sqrt{2}$ et b= $\sqrt{2}$ conviennent.
Sinon les nombres $a = {\sqrt{2}}^{\sqrt{2}}$ et $b = \sqrt{2}$ sont irrationnels et $a^{b}$ vaut 2.

Exercice 1. Démontrer que pour tout entier naturel $n$ , les nombres entiers $n^{2} + 3 n$ et $n (7 n + 1)$ sont pairs.

Exercice 2. Disjonction de cas et table de vérité.
Comparer, à l'aide d'une table de vérité, les assertions $[(𝒫 OU 𝒬) \Rightarrow ℛ$ ] et [ $(𝒫 \Rightarrow ℛ)$ ET $(𝒬 \Rightarrow ℛ)$ ].

Méthode par exhaustion

Un raisonnement par disjonction des cas vise à établir le même résultat dans tous les cas rencontrés. Il existe une autre catégorie de problèmes où l'on traite les diverses situations se produisant, mais qui conduisent à des réponses non nécessairement identiques. Dans ce cas, on parlera plutôt de méthode par exhaustion ou méthode exhaustive.

Exemple. Trois frères Alfred, Bernard et Claude ont des crayons de couleur différente bleu, rouge et vert. De plus, les assertions suivantes sont vraies :

Si le crayon d'Alfred est vert, alors le crayon de Bernard est bleu.
Si le crayon d'Alfred est bleu, alors le crayon de Bernard est rouge.
Si le crayon de Bernard n'est pas vert, alors le crayon de Claude est bleu.
Si le crayon de Claude est rouge, alors le crayon d'Alfred est bleu.

Que peut-on conclure sur la couleur respective des crayons d'Alfred, Bernard et Claude? Y a-t-il plusieurs possibilités ?

Aide. Faites l'hypothèse que le crayon d'Alfred est vert et voyez ce qu'on peut en déduire. Si vous en déduisez que le crayon d'un autre est à la fois de deux couleurs différentes ou que deux des frères ont des crayons de même couleur, c'est que cela n'est pas possible. Faites alors une autre hypothèse.

Solution. Le crayon d'Alfred est rouge, celui de Bernard est vert et celui de Claude est bleu.

Exercice. Un scénario de Lewis Caroll
Considérons le problème suivant sachant que chacune des assertions suivantes est vraie :

Ou le malfaiteur est venu en voiture, ou le témoin s'est trompé ;
Si le malfaiteur a un complice, alors il est venu en voiture ;
Le malfaiteur n'avait pas de complice et n'avait pas la clé ou bien le malfaiteur avait un complice et avait la clé ;
Le malfaiteur avait la clé.

Que peut-on en conclure ? Si on remplace la dernière par le malfaiteur n'avait pas la clé, peut-on conclure ?

Raisonnement par analyse-synthèse

Le raisonnement par analyse-synthèse s'utilise souvent dans la recherche d'un ensemble d'éléments vérifiant une propriété $𝒫$ . On l'utilise également lorsqu'on ne fait pas de raisonnement par équivalence, dans le but d'arriver au même résultat.

Le principe est le suivant:

Dans la partie analyse, on cherche les conditions nécessaires que doivent vérifier les éléments satisfaisant $𝒫$ .
Dans la partie synthèse, on s'assure que les éléments satisfaisant les conditions nécessaires obtenues dans la partie analyse vérifient bien $𝒫$ .

Exemple.
Démontrer qu'il existe un unique couple

(f, g)

de fonctions définies sur

ℝ

à valeur dans

ℝ

vérifiant les conditions :

$f$ est une fonction paire (Rappel : $f$ est paire si $\forall x \in ℝ f (- x) = f (x)$ )
$g$ est une fonction impaire (Rappel : $g$ est impaire si $\forall x \in ℝ g (- x) = - g (x)$ )
$\forall x \in ℝ, e^{x} = f (x) + g (x)$

Analyse : On suppose qu'un tel couple $(f, g)$ existe. Alors, pour tout $x \in ℝ$ , on a :

$𝒮 {\begin{array}{rcl} e^{x} = f (x) + g (x) \\ e^{- x} = f (- x) + g (- x) = f (x) - g (x) \end{array}$

En résolvant le système $𝒮$ , on obtient les (uniques) solutions :

$f (x) = \frac{e^{x} + e^{- x}}{2}$ et $g (x) = \frac{e^{x} - e^{- x}}{2}$

Synthèse : Il reste à vérifier que ces solutions vérifient bien les trois conditions imposées: $f$ paire, $g$ impaire et $\forall x \in ℝ, e^{x} = f (x) + g (x)$ , ce qui ne présente aucune difficulté et que nous laissons à faire au lecteur.

Conclusion : On a ainsi trouvé un couple ( $f, g$ ), avec $f$ paire et $g$ impaire et vérifiant $\forall x \in ℝ, e^{x} = f (x) + g (x)$ et ce couple est unique.

Principe de récurrence

Raisonnement par récurrence : On souhaite démontrer une assertion

𝒫 (n)

, pour tout entier naturel

n

, ou pour des entiers naturels

n

supérieurs à un entier naturel

n_{0}

.
Il faut d'abord bien l'énoncer... Ensuite, on suit la démarche suivante en trois étapes:

Principe de récurrence:

On montre qu'il existe un entier $n_{0}$ tel que $𝒫 (n_{0})$ soit vraie.
C'est l'initialisation en $n_{0}$ .
On montre ensuite que l'assertion : $𝒫 (n) \Rightarrow 𝒫 (n + 1)$ est vraie pour $n \geq n_{0}$ .
L'assertion $𝒫 (n)$ est dite alors héréditaire pour $n \geq n_{0}$ .
Dans la pratique, on nomme "hypothèse de récurrence" la proposition $𝒫 (n)$ que l'on suppose vraie pour un entier $n \geq n_{0}$ puis on démontre que $𝒫 (n + 1)$ est vrai.
On énonce la conclusion : Par récurrence, on montre ainsi que la proposition $𝒫 (n)$ est vraie pour tout entier $n \geq n_{0}$ .

Soyez particulièrement attentifs à la rédaction d'un tel raisonnement.

Exemple : Montrer que la somme des $n$ premiers entiers vaut : $S_{n} = 1 + 2 + 3 + . . . + n = \frac{n (n + 1)}{2}$

Initialisation. $S_{1}$ somme des nombres de 1 à 1 vaut : $S_{1} = 1 = \frac{1 (2)}{2}$ . C'est juste.
Hérédité. Soit $n \geq 1$ tel que $S_{n} = \frac{n (n + 1)}{2}$ . Montrons que : $S_{n + 1} = \frac{(n + 1) (n + 2)}{2}$

S_{n + 1} = (1 + 2 + 3 + . . . + n) + (n + 1) = S_{n} + (n + 1) = \frac{n (n + 1)}{2} + (n + 1)

(n + 1) (\frac{n}{2} + 1)

(n + 1) \frac{n + 2}{2} = \frac{(n + 1) (n + 2)}{2}

Conclusion : la propriété est vérifiée, pour tout $n \in ℕ$ .

Exercice : Montrer que la somme des carrés des $n$ premiers entiers naturels vaut : $T_{n} = 1^{2} + 2^{2} + 3^{2} + . . . + n^{2} = \frac{n (n + 1) (2 n + 1)}{6}$

Un autre exemple

D'autres exercices

Raisonnement par récurrence : un exemple

Donnons une version imagée du principe de récurence (à propos récurrence vient de courir en arrière).
Mettons 543 dominos sur une table, verticalement et proches les uns des autres. Je désire montrer que, si je fais tomber le premier domino sur le second, les 543 dominos tombent.

Propriété $𝒫 (n)$ : $\forall n \geq 2, n \leq 543$ les $n$ premiers dominos sont tombés.

D'une part $𝒫 (2)$ est vraie car si je fais tomber moi-même le premier domino sur le second, celui-ci tombe, et les deux premiers sont tombés.
D'autre part, l'assertion $𝒫 (n) \Rightarrow 𝒫 (n + 1)$ est vraie.
En effet si le $n$ -ième est tombé, il est tombé sur le $(n + 1)$ -ième qui tombe à son tour, alors les $n + 1$ dominos premiers sont donc tombés.
L'initialisation et l'hérédité sont prouvées, et par récurrence on a prouvé la proposition $𝒫 (n)$ , pour $n$ compris entre 2 et 543.

Dans le détail du principe de récurrence :
Comme $𝒫$ (2) et $(𝒫 (2) \Rightarrow 𝒫 (3)$ ) sont vraies, $𝒫 (3)$ est vraie.
Comme $𝒫$ (3) ) et [ $𝒫 (3) \Rightarrow 𝒫 (4)$ ] sont vraies, $𝒫 (4)$ est vraie.
.........................
Comme $𝒫$ (542) et [ $𝒫 (542) \Rightarrow 𝒫 (543)$ ] sont vraies, $𝒫 (543)$ est vraie et les 543 dominos sont tombés.

Conclusion : "Si je fais tomber le premier domino sur le second, les 543 dominos tombent".

Remarquons que si j'avais fait tomber le premier domino de l'autre côté, l'implication $𝒫 (n) \Rightarrow 𝒫 (n + 1)$ serait toujours vraie, en revanche $𝒫 (2)$ ne le serait pas... Donc $𝒫 (543)$ ne serait pas vraie (en tout cas sans autre hypothèse et si votre animal préféré arrive, je ne réponds plus de rien).

Récurrence : Exercices

Exercice 1:
À partir de quel rang les quatre propriétés suivantes sont-elles héréditaires? ?
Peut-on les initialiser, et à partir de quel rang ?

Dans les cas suivants, l'assertion $𝒫 (n)$ est-elle héréditaire pour tout entier naturel $n$ ? Les propositions $𝒫 (0), 𝒫 (1), 𝒫 (2)$ sont-elles vraies ? La proposition $𝒫 (n)$ est-elle vraie pour tout entier naturel $n$ ? La proposition $𝒫 (876)$ est-elle vraie ?

$𝒫 (n)$ : $n + 1 < n$
$𝒫 (n)$ : $n^{3} \leq n^{2}$
$𝒫 (n)$ : $10^{n} - (- 1)^{n}$ est divisible par 11
$𝒫 (n)$ : $10^{n} + 1$ est divisible par 9

Exercice 2: Montrez l'inégalité: $2^{n} > n^{2}$ . Que pensez-vous de l'énoncé ? Précisez-le et proposez un énoncé correct. Démontrez-le.

Indication : On s’apercevra que l'initialisation ne peut commencer qu'a partir de

n = 6

, et on prouvera qu'en revanche l'hérédité débute à

n = 2

Une récurrence fausse

Il arrive que l'on fasse une mauvaise hypothèse de récurrence, que la propriété soit fausse pour le

n_{0}

choisi, ou que la preuve de l'hérédité ne soit pas valide pour tout

n

. Trouvez l'erreur dans cette "démonstration" de l'assertion

Tous les crayons de couleur d'une même boîte sont de même couleur.

"Pseudo-démonstration".

Si la boîte ne contient qu'un seul crayon, tous les crayons de la boîte sont de même couleur. La propriété est donc initialisée.
Prenons comme hypothèse de récurrence :
Tous les crayons d'une boîte de $k$ crayons sont de même couleur.
Prenons une boîte de crayons contenant $k + 1$ crayons. Enlevons le crayon $A$ , par exemple. Par hypothèse de récurrence, les $k$ crayons de couleur qui restent ont la même couleur.
Remettons $A$ et enlevons un autre, $B$ . Par hypothèse de récurrence, les $k$ crayons de couleur qui restent ont la même couleur que $A$ . Et, d'après ce qui précède, ils ont aussi la même couleur que $B$ .
Donc les $k + 1$ crayons de couleur sont tous de la même couleur. L'hérédité est donc "prouvée"
Conclusion : Tous les crayons de couleur d'une même boîte sont de la même couleur.

Bien évidemment, il se trouve une erreur quelque part... Trouvez-la !

Récurrence double

Parfois l'hérédité se démontre non pas uniquement par rapport au rang précédent, mais par rapport aux deux précédents. On parle alors de récurrence double. La démarche doit alors être légèrement modifiée.
On souhaite démontrer une assertion

𝒫 (n)

pour des entiers naturels

n

supérieurs à un entier naturel

n_{0}

Règle:

Initialisation en $n_{0}$ , on montre que $𝒫 (n_{0})$ et $𝒫 (n_{0} + 1)$ sont vraies.
On montre ensuite que l'assertion : [ $𝒫 (n)$ et $𝒫 (n + 1)] \Rightarrow 𝒫 (n + 2)$ , est vraie pour $n \geq n_{0}$ .
L'assertion $𝒫 (n)$ est alors héréditaire pour $n \geq n_{0}$ .
Conclusion: par le principe de récurrence, on a montré que $𝒫 (n)$ est vraie, pour tout entier $n \geq n_{0}$ .

Exemple. On considère la suite dite de "Fibonacci", définie par :

$u_{0} = 1, u_{1} = 1$ et $\forall n \in ℕ, u_{n + 1} = u_{n} + u_{n - 1}$

Montrer que l'inégalité suivante est vraie :

$\forall n \in ℕ u_{n} \leq {(\frac{7}{4})}^{n}$

Les deux inégalités suivantes sont vraies : $u_{0} = {(\frac{7}{4})}^{0} = 1 \leq \frac{7}{4}$ , et $u_{1} = {(\frac{7}{4})}^{1} = \frac{7}{4} \leq \frac{7}{4}$ .
Soit $n \in ℕ^{*}$ , vérifiant les deux inégalités :
$u_{n} \leq {(\frac{7}{4})}^{n}$ et $u_{n - 1} \leq {(\frac{7}{4})}^{n - 1}$ .
Alors : $u_{n + 1} = u_{n} + u_{n - 1} \leq {(\frac{7}{4})}^{n} + {(\frac{7}{4})}^{n - 1}$
$u_{n + 1} \leq {(\frac{7}{4})}^{n - 1} (\frac{7}{4} + 1) \leq {(\frac{7}{4})}^{n - 1} (\frac{44}{16}) \leq {(\frac{7}{4})}^{n - 1} (\frac{49}{16}) \leq {(\frac{7}{4})}^{n + 1}$
Par le principe de récurrence, le résultat est ainsi démontré, pour tout $n$ dans $ℕ$

Exercice. Soit

x \in ℝ^{*}

, tel que

x + \frac{1}{x} \in ℤ

Montrer par une récurrence double que, $\forall n \in ℕ, x^{n} + {(\frac{1}{x})}^{n} \in ℤ$
Question annexe : trouver un réel $x$ , non entier, vérifiant l'hypothèse.

Bibliographie

F. Liret et D. Martinais, Mathématiques pour le DEUG, Algèbre 1ère Année (Dunod), chapitre 1
A. Auzimour et F. Petit, Travaux dirigés d'algèbre (Vuibert)
A. Denmat et F. Héaulme, Algèbre générale (Dunod), td 1

une introduction aux raisonnements.
: reasoning,math_symbols,quantifier, implication, contraposition, truth_table, recurrence, interactive mathematics, interactive math, server side interactivity, qcm, sciences, language,courses

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.

Raisonnements

Sommaire

Langage mathématique

Raisonnements

Bibliographie

Langage mathématique

Expressions mathématiques

Exemples d'expressions mathématiques

Assertions ou Propositions

Connecteurs : NON, ET et OU

Implication, équivalence

Négation d'une assertion utilisant un connecteur

Condition nécessaire, condition suffisante.

Négation d'une assertion utilisant des quantificateurs

Contraposée et réciproque

Contraposée et réciproque : pièges de la vie courante

Raisonnements

Raisonnement par implication

Raisonnement par équivalence

Raisonnement par équivalence en deux temps.

Raisonnement par contraposition

Raisonnement par l'absurde

Raisonnement par disjonction des cas

Méthode par exhaustion

Raisonnement par analyse-synthèse

Raisonnement par récurrence

Principe de récurrence

Raisonnement par récurrence : un exemple

Récurrence : Exercices

Une récurrence fausse

Récurrence double

Bibliographie