Systèmes dynamiques
--- Introduction ---
Ce module regroupe pour l'instant 17 exercices sur les systèmes
dynamiques réels.
Évolution du capital
On dispose d'un compte d'épargne à un taux de %, avec une inflation de %.
L'évolution dans le temps du pouvoir d'achat est donnée par une application
.
Le graphe du pouvoir d'achat est représenté en rouge sur 50 ans. Au bout de combien de temps ? (cliquez sur l'axe du temps)
Dynamique symbolique I
(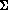 ,
,  ) est le système dynamique à 2 symboles où :
) est le système dynamique à 2 symboles où : -
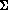 , est l'ensemble des suites infinies
avec
égal à 0 ou 1.
, est l'ensemble des suites infinies
avec
égal à 0 ou 1. -
est le décalage (vers la droite),
.
Parmi les éléments de 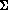 , notons
, notons 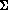 ' l'ensemble des suites telles que si
, alors
' l'ensemble des suites telles que si
, alors
,
Combien y-a-t-il de points fixes de
dans
?
Donner le point fixe :
Combien y-a-t-il des points de période exactement 2 de
dans
?
Donner les deux points de période 2 :
Combien y-a-t-il des points de période exactement 3 de
dans
?
Donner les trois points de période 3 :
On écrit un point de période
sous la forme
.
Par exemple,
représente la suite (1,1,1,1,...),
représente la suite (1,0,0,1,0,0,1,0,0,1,0,0...).
Dynamique symbolique II
(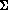 ,
,  ) est le système dynamique à 2 symboles où :
) est le système dynamique à 2 symboles où : -
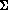 , est l'ensemble des suites infinies
avec
égal à 0 ou 1.
, est l'ensemble des suites infinies
avec
égal à 0 ou 1. -
est le décalage (vers la droite),
.
Parmi les éléments de 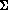 , notons
, notons 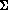 ' l'ensemble des suites telles que si
, alors
' l'ensemble des suites telles que si
, alors
.
Combien y-a-t-il de points fixes de
dans
?
Donner le point fixe :
Combien y-a-t-il de points de période exactement 2 de
dans
?
Donner les deux points de période 2 :
Combien y-a-t-il de points de période exactement 3 de
dans
?
Donner les trois points de période 3 :
Combien y a-t-il de points fixés par
?
de points fixés par
?
Combien y a-t-il de points de période exactement 4 de  ?
de période exactement de
?
de période exactement de  ?
?
On écrit un point de période
sous la forme
.
Par exemple,
représente la suite (1,1,1,1,...),
représente la suite (1,0,0,1,0,0,1,0,0,1,0,0...).
Points fixes
Soit
une application de l'intervalle. Les graphes de
(gauche) et de
(droite) sont représentés en rouge.
Combien de points fixes
a-t-elle ?
L'application
n'a pas de points fixes.
a
point fixe.
points fixes.
Parmi eux, combien de points sont-ils attractifs ?
Aucun de ces points n'est attractif.
Exactement, parmi ces points
est attractif.
sont attractifs.
Combien de points périodiques de période exactement 2
a-t-elle ?
Aucun de ces points n'est périodique de période exactement 2.
L'application
if{a exactement }
point périodique.
points périodiques.
de période exactement 2.
Combien de points périodiques de période exactement 2
a-t-elle ?
L'application
n'a pas de points périodiques de période exactement 2.
a exactement
point périodique
points périodiques
de période exactement 2.
Parmi eux, combien de points sont-ils attractifs ?
Parmi eux, combien de points sont-ils attractifs ?
Famille polynomiale en degré 3
Soit
l'application de
dans
définie par
Quels sont les points fixes de
Les points fixes de
sont .
Que vaut
aux points fixes dans  :
:
,
,
Parmi tous les points fixes, lesquels sont attractifs ?
Parmi tous les points, lesquels sont répulsifs ?
On recherche des points périodiques de période 2 ; en particulier quels sont les points
non nuls tels que
?
Parmi les points suivants (périodiques de période 2), lesquels sont répulsifs ?
Ecrire ø pour l'ensemble vide.
Ecrire , pour les infinis.
Portrait de phase
Soit
une application de l'intervalle. Son graphe est représenté en rouge.
Pour un
, quelle est l'écriture de
?
Quelle est la valeur du paramètre
pour laquelle
?
La transformation
identifie l'intervalle
au cercle et l'application
à un homéomorphisme du cercle.
Quel est le portrait de phase de cet homéomorphisme ?
Point fixe attractif
Soit
une application de l'intervalle (graphe rouge). Indiquez le point fixe attractif en cliquant sur le graphe.
Famille quadratique I
Soit
l'application de
dans
donnée par
.
Les points fixes de
sont
Pour chacun des points fixes, donner la dérivée de
en ce point et dire s'il est attractif ou répulsif :
| point | dérivée | attractif/répulsif |
|---|
| 0 |
|
|
|---|
|
|
|
|---|
Famille quadratique II
Soit
l'application de I =
dans
donnée par
.
Certains points de l'intervalle I s'en échappent après itérations de
. L'ensemble des points de
qui s'échappent en
au plus
exactement
itération
itérations
est composé de
intervalles.
Certains points de I s'échappent de
après itérations de
. L'ensemble des points de
qui s'échappent en
au plus
exactement
itérations est composé de intervalles. Parmi ces intervalles, donner celui qui est le plus proche de :
,
L'application quadratique 4x(1-x)
Soit l'application de
segments black, 0,0,1,1
On code l'itinéraire d'un point
de
différent de
sous l'action de
pour
pour
,
pour
Pour
, on lui associe une adresse au temps
1. Quelle est l'adresse de
au temps
?
Quels sont les points périodiques de
de période
au plus
exactement
Donner les adresses des points périodiques
de période
au plus
exactement
au temps :
Rotations
Soit
la rotation du cercle d'angle
, où
.
L'application
est-elle périodique ?
Quelle est la période de
?
Indiquez la représentation correcte de la dynamique sur l'orbite périodique de
Application standard avec bruit I
L'application
de l'intervalle [ 0, 1 ] dans lui-même dont le graphe est représenté ci-dessous en rouge est de la forme
modulo 1
avec
( , a) =
, a) =
et
=
( , a) = (,) et
, a) = (,) et
La transformation
identifie l'intervalle [ 0, 1] au cercle de centre
et de rayon
et l'application
à un homéomorphisme du cercle.
Parmi les points gris représentés sur le cercle, cliquer sur ceux appartenant à l'image par la transformation
de l'orbite de
sous
.
L'orbite de
sous
est
.
Application standard avec bruit II
L'application
de l'intervalle [ 0, 1 ] dans lui-même dont le graphe est représenté ci-dessous en rouge est de la forme
modulo 1
avec
(

, a) =
et
=
( , a) = (,) et
, a) = (,) et
La transformation
identifie l'intervalle [ 0, 1] au cercle de centre
et de rayon
et l'application
à un homéomorphisme du cercle.
Parmi les points gris représentés sur le cercle, cliquer sur ceux appartenant à l'image par la transformation
de l'orbite de
sous
.
L'orbite de
sous
est
.
L'application tente
Soit I l'intervalle
= [0, 1]. Soit l'application de
dans
dont le graphe est représenté en rouge.
segments black,0,0,1,1
On code l'itinéraire d'un point
de
différent de
sous l'action de
pour
pour
,
pour
Pour
, on lui associe une adresse au temps
Quelle est l'adresse de
au temps
?
Quels sont les points périodiques de
de période exactement
?
3. - Donner les adresses au temps des points périodiques de
de période exactement
| |
|
Trajectoires
Soit
la rotation du cercle d'angle
. On représente la dynamique sur l'orbite périodique de
pour plusieurs valeurs de
. Identifiez les correspondances entre ces valeurs de
et les trajectoires de
.
Types de point fixe
Soit
,
une application qui définit un système dynamique sur
, où
. Son graphe est tracé en rouge sur l'intervalle
.
Indiquez les points fixes de
dans
est un point fixe
est un point fixe
Le bassin d'attraction du point fixe est
Applications unimodales
Soit
une application de l'intervalle (graphe rouge).
Écrire les abscisses (à
près) des points fixes de
La droite tracée en vert est la tangente de
au point fixe . Indiquez le type du point fixe :
En utilisant éventuellement l'orbite critique (tracée en bleu), identifiez le graphe de l'application
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: collection d'exercices sur les systèmes dynamiques réels en dimension 1. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, qcm, sciences, language,courses, analysis, topology, dynamique réelle, point périodique, periodicité, dynamic_system
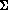 , est l'ensemble des suites infinies
avec
égal à 0 ou 1.
, est l'ensemble des suites infinies
avec
égal à 0 ou 1. 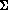 ,
,  ) est le système dynamique à 2 symboles où :
) est le système dynamique à 2 symboles où : 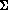 , est l'ensemble des suites infinies
avec
égal à 0 ou 1.
, est l'ensemble des suites infinies
avec
égal à 0 ou 1. 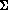 , notons
, notons 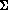 ' l'ensemble des suites telles que si
, alors
' l'ensemble des suites telles que si
, alors 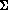 ,
,  ) est le système dynamique à 2 symboles où :
) est le système dynamique à 2 symboles où : 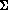 , est l'ensemble des suites infinies
avec
égal à 0 ou 1.
, est l'ensemble des suites infinies
avec
égal à 0 ou 1. 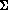 , notons
, notons  ' l'ensemble des suites telles que si
, alors
' l'ensemble des suites telles que si
, alors  ?
de période exactement de
?
de période exactement de  ?
?
 :
: , a) =
, a) =
 , a) = (,) et
, a) = (,) et
 , a) =
, a) =
 , a) = (,) et
, a) = (,) et