OEF vektorski podprostori
--- Uvod ---
Ta modul trenutno vsebuje 8 vaj o podprostorih
v vektorskih prostorih.
Razsežnost preseka
Naj bo U vektorski prostor razsežnosti , in naj bosta
,
njegova podprostora razsežnosti in . Potem je razsežnost preseka
enaka najmanj
in največ
.
Homogeni lin. sistem in razsežnost
Naj bo V podprostor vektorskega prostora R, ki ga določa sistem homogenih linearnih enačb, katerega matrika sistema ima rang . Določite razsežnost prostora V.
Razsežnost vsote
Naj bo U vektorski prostor razsežnosti in naj bosta
,
njegova podprostora razsežnosti in . Potem je razsežnost vsote
enaka najmanj
in največ
.
Podbaza
Naj bo U vektorski prostor razsežnosti in množica B njegova baza. Denimo, da je
njena podmnožica moči , ki določa podprostor V prostora U. Potem je razsežnost dim(U) enaka
.
Podbaza II
Naj bo U vektorski prostor razsežnosti in naj bo B njegova baza. Denimo, da sta
in
dve podmnožici množice B z močjo oziroma , njun presek
pa ima moč . Naj bosta
in
podprostora v U z ogrodjema
oziroma
. Potem je razsežnost preseka
enaka
.
Razsežnost podprostora
Naj bo V vektorski podprostor prostora  , . Potem je razsežnost dim(V) enaka
.
, . Potem je razsežnost dim(V) enaka
.
Razsežnost podprostora matrik
Naj bo V vektorski podprostor prostora  ×, ki vsebuje vse realne × matrike A, za katere velja =0 za neko izbrano neničelno matriko B velikosti ×. Potem je njegova razsežnost dim(V) enaka najmanj
in največ
.
×, ki vsebuje vse realne × matrike A, za katere velja =0 za neko izbrano neničelno matriko B velikosti ×. Potem je njegova razsežnost dim(V) enaka najmanj
in največ
.
Razširitev podprostora
Naj bo V vektorski prostor razsežnosti dim(V)= in U njegov podprostor razsežnosti dim(U)= z ogrodjem S. Naj bo v 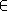 V vektor, ki linearna kombinacija vektorjev iz S, in naj bo U' vektorski podprostor v F z ogrodjem
{v}. Kolikšna je razsežnost prostora U'?
The most recent version
V vektor, ki linearna kombinacija vektorjev iz S, in naj bo U' vektorski podprostor v F z ogrodjem
{v}. Kolikšna je razsežnost prostora U'?
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent ętre utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: zbirka vaj o vektorskih podprostorih. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, qcm, sciences, language,courses, algebra, linearna algebra, vektorski prostor, podprostor, baza, razsežnost, linearni sistem
 , . Potem je razsežnost dim(V) enaka
.
, . Potem je razsežnost dim(V) enaka
.
 ×, ki vsebuje vse realne × matrike A, za katere velja =0 za neko izbrano neničelno matriko B velikosti ×. Potem je njegova razsežnost dim(V) enaka najmanj
in največ
.
×, ki vsebuje vse realne × matrike A, za katere velja =0 za neko izbrano neničelno matriko B velikosti ×. Potem je njegova razsežnost dim(V) enaka najmanj
in največ
.
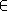 V vektor, ki linearna kombinacija vektorjev iz S, in naj bo U' vektorski podprostor v F z ogrodjem
{v}. Kolikšna je razsežnost prostora U'?
V vektor, ki linearna kombinacija vektorjev iz S, in naj bo U' vektorski podprostor v F z ogrodjem
{v}. Kolikšna je razsežnost prostora U'?